
"Vannak népek, amelyek tízesével, mások húszasával számolnak. Sokszor ismételt gondolat, hogy a tízes alapú számrendszerek valahogy logikusabbak, a két kéz ujjai miatt. A kaliforniai yukik állítólag ugyanezen megokolással úgy vélik, hogy az ő nyolcas alapú számrendszerük a legmegfelelőbb. Ők ugyanis az ujjaik közötti rést veszik alapul."
Reuber Hersh: A matematika természete
Typotex Kiadó, 2000
241. oldal
Nem érdekel a matematika.* Az emberi gondolkodás érdekel**.
Ez a könyv az emberi gondolkodás történetének egy speciális aspektusával foglalkozik. Azzal, hogy:
Mit gondoltak és gondolnak a matematikusok és a filozófusok és a matematikus-filozófusok a matematikáról?
Röviden összefoglalva*** a 350 oldalas könyvet, Reuben Hersh szerint a matematika-filozófia művelői ahányan vannak, annyi félét mondanak (nincs közmegegyezés), de azért a különböző gondolkodásmódok egymásra épülnek, összefüggnek, és néhány főbb trend kirajzolódik.
A legáltalánosabb, a matematika tudományának kialakulásáig visszanyúló felfogás platonista, idealista (a számok és szabályaik örök, embertől független ideák).
Ezzel szemben fellép egy racionalista, formalizmusra törekvő irányzat (a matematika formalizált szabályokkal leírható-leírandó logikus módszer vagy játék, akár egy nyelv).
E két megközelítési mód (szerintem) nyilvánvalóan összefügg az ember-Isten(ek), ember-tudat kapcsolatokra adott, koronként változó (szerintem fejlődő) válaszokkal.
A probléma kapcsán megnyilatkozik többek között (a részletesebben tárgyaltakból sorolok): Püthagorasz, Platon, Arisztotelész, Szent Ágoston, Descartes, Spinoza, Leibniz, Berkeley, Kant, Locke, Hume, d'Alembert, Mill, Gottlob Frege, Bertrand Russel, Brouwer, Kurt Gödel, David Hilbert, Rudolph Carnap, Wittgenstein, Poincare, Hilbert, Lev Vigotszkij, Rényi, Polányi, Pólya, Lakatos, Karl Popper, Mario Bunge, Philip Kitcher, Jean Piaget, Paul Ernest, Thomas Kuhn és a Bourbaki csoport. Elég jó kis névsor.
Mindeközben az egyszerű, hétköznapi (elméleti- vagy alkalmazott matematikát művelő) matematikusok leginkább számolnak, modelleznek, intuícióik alapján feltételeznek és bizonyítani törekednek, konkrét problémákat akarnak megoldani, mit sem törődve a teóriákkal. Nyilván igazuk van, a matematika matematika-filozófia nélkül is művelhető.
A szerző válasza a feltett kérdésre (a saját interpretációmban):
A matematika sem nem fizikai, sem nem mentális, hanem társadalmi tény. A matematikát nem írhatjuk le kizárólag fizikai jellemzőkkel, centiméterben és kilogrammban, de kizárólag mentális jellemzőkkel sem, például szokások és reflexek összességeként. Csak társadalmi, kulturális, történelmi összefüggésekben van értelme beszélni róla. Test nélkül nincs tudat, test és tudat nélkül nincs társadalom, kultúra és történelem. A társadalom, a kultúra, a történelem mentális és fizikai szinteken alapszik, azonban vannak olyan tulajdonságaik, amelyek az alapszintből nem megmagyarázhatóak. Ez analóg a matematikával. A matematika a fizikai világban létező, fizikai testben (az emberi agyban) keletkező egyéni tudatokból, mentális tartalmakból összeálló kollektív ismeretrendszer, amely időben változó, történelmi, társadalmi, kulturális hatásoknak kitett formákban és szabályokban jelenik meg.
Ez Reuben Hersh meghatározása szerint a humanista matematikafilozófia. (Nekem tetszik.)
A könyv három részből áll. Az első részben a matematika-filozófia elveinek elemzését adja. A második részben áttekinti a különböző filozófusok matematikára vonatkozó elméleteit, és megfogalmazza a saját teóriáját. A harmadik részben a különböző matematika-filozófiák társadalmi-politikai hatásáról ír, valamint 70 oldalban matematikai levezetéseket, bizonyításokat közöl (például Gödel nem teljességi tételének egy speciális bizonyítását), amelyekre az előző két fejezetben hivatkozott.
Érdekes, elgondolkodtató és néhol vitára ingerlő, alaposabb matematikai ismeretek nélkül is érthető, filozófiai szakkönyv.
* Nem vagyok elég okos hozzá. Esténként, munka után, nem szoktam matematikai problémák megoldásán törni a fejem, hobbiból egyenleteket, szöveges feladatokat megoldani, deriválni, integrálni, logikai kérdésekre geometriai szerkesztések segítségével választ keresni. Az érdeklődés hiánya nyilván abból fakad, hogy nem ismerem fel a matematika szépségeit. Nem vagyok elég okos hozzá, nem jutok el addig a szintig, hogy érzékeljem a problémák komplexitását és a megoldások eleganciáját.
Van egy privát teóriám, amely szerint a természettudósok, a fizikusok, kémikusok, biológusok és a matematikusok okosabbak, mint a humán területek tudósai. (Annak ellenére, hogy állítólag Einstein, amikor egy Kafka könyvet adtak elolvasásra neki, azzal adta vissza, hogy nem érti, és szerinte az emberek nem gondolkoznak ennyire bonyolultan.) Talán csak a filozófusok között vannak kivételek.
Itt, persze, az a kérdés merül fel, hogy mit értünk okosság alatt? Az okosság, szerintem, leginkább a memória kapacitását, az általánosítás és elvonatkoztatás, valamint az ezeken alapuló invenció képességét jelenti. Ezen biztosan lehetne vitatkozni.
** Ismerni akarom saját lehetőségeimet és korlátaimat. Ezen túl, meg akarom érteni a feleségemet, az aktuális kormányfő politikai beszédének indítékait, a homeopátiát propagáló orvosokat, a toleráns vagy fundamentalista vallásosokat, a posztmodern filozófusokat, satöbbi. Ezek nyilván nem azonos súlyú problémák, de most éppen ilyenek foglalkoztatnak.
*** Lásd még: Hogyan tanuljunk meg könnyen, gyorsan kínaiul?
A képen Platón és Arisztotelész
"…Arisztotelésznek „elég rossz a sajtója”. Megtudhatjuk, hogy a modern tudomány születése ahhoz a küzdelemhez köthető, amelyet Galilei, Kopernikusz és Descartes vívott Arisztotelész és Aquinói Szent Tamás ellen. A történelem persze sokkal bonyolultabb ennél. Az európai filozófiai gondolkodás nagyrészt a platonisták és arisztoteliánusok összecsapásában fejlődött ki. Szent Ágoston korától (ötödik század) kezdve Platón az egyházi dogma része volt. Arisztotelész írásai évszázadokon keresztül eltűntek Nyugat-Európából. A tizenkettedik században tértek csak vissza, észak-afrikai és spanyolországi arab tudósoknak köszönhetően.
[…]
Arisztotelész matematika-filozófiájának központi fogalma az absztrakció. A számokat és geometriai alakzatokat a fizikai tárgyakból absztraháljuk, ha irreveláns tulajdonságaiktól – színtől, helytől, értéktől, stb. – elvonatkoztatunk, hogy (mértani alakzatoknál) már csak a nagyság és forma marad, (a véges halmazok esetében) pedig a „számosság”. Az elemi matematika leírásaként nem is rossz."
Reuber Hersh: A matematika természete
Typotex Kiadó, 2000
241. oldal
"A politikai konzervativizmus ellenzi a változást. A matematikai platonizmus azt vallja, a matematika nem változik. A politikai konzervativizmus az elitet az egyszerű emberek fölé helyezi. A matematikatanításban a platonizmus azt sugallja, a diák vagy képes belátni a matematikai igazságokat, vagy nem.
A humanista, avagy társas-konstruktivista, avagy társas-konceptualista, avagy kvázi-empirista, avagy naturalista, avagy deviáns matematikafilozófia a fejéről a talpára állítja a matematikát. Ez összhangban van a balos elit-ellenességgel, az analfabetizmus leküzdésének, az egyetemi képzés általánossá tételének, a tudás és kultúra általános terjesztésének történelmi küldetésével. Ilyen meglepő lenne, hogy a platonisták számfogalma a politikai konzervativizmussal kapcsolható össze, a humanisták számfogalma viszont a demokratikus politikával?"
Reuber Hersh: A matematika természete
Typotex Kiadó, 2000
258-259. oldal
Ez az idézet az Összegzésés értékelés című fejezetből való. Reuber Hersh fejéről a talpára akarja állítja a matematikát, és történelmi küldetésről beszél – ezek erősen átideologizált kifejezések, amelyek a marxizmust idézik és elég elidegenítően hatnak, de a szerző biztosan nem marxista, „csak” baloldali, humanista materialista.
Reuber Hersh odáig is elmegy, hogy kategorizálja a filozófusokat, matematikusokat. Indoklásokat is fűz hozzá, ezeket nem idézem, mert hosszú, csak a végeredményt:
"A fő vonulatba tartozik [tehát a platonizmust képviseli] Püthagorasz, Platon, Augustinus, Nicolaus Cusanus,
Descartes, Berkley, Leibniz, Frege, Brouwer és Quine a JOBB OLDALON [a nagybetűs kiemelések tőlem]; Spinoza, Kant és Russel a BAL OLDALON. Összesen 10 jobbos, három balos.
Nézzük a humanistákat. […]
Ha a besorolhatatlan Peirce-t, Poincarét, Hilbertet és Wittgensteint kihagyjuk, a humanisták között a BAL OLDALON ott találjuk Arisztotelészt, Locke-ot, Hume-ot, d'Alembert-t, Millt, Rényit, Polányit és Pólyát, a JOBB OLDALON pedig Aquinói Tamást és Lakatost. A mérleg tehát 8 balos és kettő jobbos.
Elmondhatjuk tehát, hogy a fősodor inkább jobbos, a humanisták inkább balosak."
Korábban találkoztam már egy olyan cikkel is, amelyik a zeneszerzőket kategorizálja politikai nézeteik alapján, innen való ez az ábra:
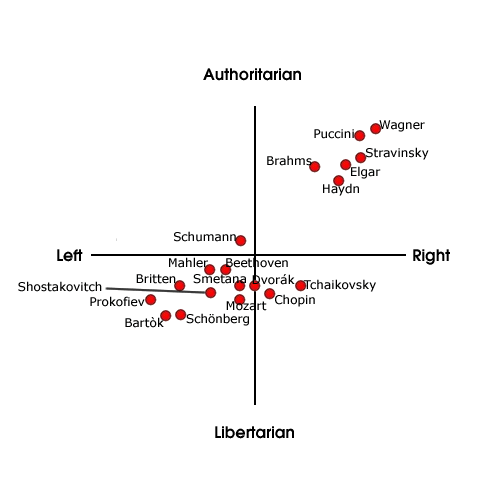
"1. A matematika emberi. Része az emberi kultúrának.
2. A matematikai tudás nem tévedhetetlen. A tudományokhoz hasonlóan a matematika gyakran hibákból tanulva halad előre, újra meg újra kiigazítva őket. (Lakatos Bizonyítások és cáfolatok című könyvében kitűnően nyomon követi ezt a jelenséget.)
3. Az időtől, helytől és egyebektől függően a bizonyításnak és szabatosságnak különböző formái léteznek. Példának okáért a számítógépek felhasználása a bizonyításban hagyományosan nem tekintendő szabatos eljárásnak. Pedig az empirikus bizonyítékok, a numerikus kísérletek és a valószínűség-számításon alapuló bizonyítások egyaránt eligazítanak a tekintetben, mit hihetünk el a matematikában. Az arisztotelészi logika a döntés nem feltétlenül egyetlen lehetséges módja.
4. A matematikai objektumok a társadalmi-történeti objektumok behatárolható részhalmazát képezik. A kultúra egy sajátos részét alkotják. Az irodalom, a vallás, a bankügyletek szintén a kultúra sajátos részei. Mind jelentősen különböznek egymástól."
Reuber Hersh: A matematika természete
Typotex Kiadó, 2000
23-24. oldal
"A vallás nem általában hanyatlik. A fundamentalizmus burjánzik, mint valami kártékony gyomnövény. Értelmiségi körökben egyaránt találkozunk Buber, Kierkegaard, Maharishi és Nágárdzsuna követőivel. A tudományban azonban többé nem játszik szerepet a vallás. Newton azt mondta, felfedezései csak Isten dicsőségét növelik, Lalplace azonban már úgy nyilatkozik Napóleon előtt, hogy Isten hipotézisét szükségtelennek tartja. A mai tudós, még ha templomba, vagy shulba jár is, álmában sem gondolna arra, hogy Isten akaratával magyarázza a mikrobiológia vagy a részecskefizika valamelyik talányát."
Reuber Hersh: A matematika természete
Typotex Kiadó, 2000
130-131. oldal
"A matematika formalista filozófiájának lényegét gyakran egy rövid jelmondattal intézik el: „A matematika egy értelmetlen játék.” (Az „értelmetlen” és „játék” szavak jelentését persze homály fedi.) […]
Mit érthetnek a formalisták „játék” alatt, ha a matematikát játéknak nevezik? Meglehet abban az értelemben használják, hogy valami, „amit szabályok szerint játszanak”. (Most a „játszani” és a „szabály” szavakat hagyjuk definiálatlanul!) […]
A szabályok lehetnek előre megállapított szabályok, mint a Monopoly-ban vagy a Scrabble-ben, illetve spontán szabályok, például a természetes nyelvek vagy az elemi artimetika szabályai. A szabályok létrehozása egyik esetben sem követ szabályokat!
Wittgenstein és még néhány láthatólag úgy vélik, hogy mivel a szabályok megalkotása szabályok nélkül megy végbe, ezért a szabályok önkényesek. Ez durva hiba, mert még számos más lehetőség is fennáll.
A nyelv és a matematika szabályait történetileg a társadalom határozza meg – mely az egyes társadalmi csoportok belső mozgása és egymás közötti interakciói hatására fejlődik –, valamint a Föld által biztosított fizikai és biológiai környezet. A társadalmi rétegeket folyamatosan alakítják az emberi egyedek biológiai tulajdonságai, különösképpen az egyén idegrendszere. Az ember biológia tulajdonságai és idegrendszere tették lehetővé a faj kialakulását és fennmaradását a Földön, így természetesen valamilyen módon visszatükrözik e bolygó fizikai és biológiai tulajdonságait. Mindez nyilvánvalóan nagyon bonyolult. Rejtélyes is – kétségtelen. De semmiképpen nem önkényes."
Reuber Hersh: A matematika természete
Typotex Kiadó, 2000
7-8. oldal
"Mi különbözteti meg a matematikát a humán tudományoktól? A matematika és az irodalomtudomány között az az alapvető különbség, hogy a matematika tárgyát tekintve ugyan humán jellegű (mivel társas jellegű fogalmakkal dolgozik), objektivitását tekintve inkább tudományos. A fizikai világra vonatkozó reprodukálható eredményeket (amik minden mérésnél vagy kérdésfeltevésnél ugyanazok) tudományosnak hívjuk. Azokat a tématerületeket pedig, amelyek reprodukálható eredményeken alapulnak, természettudományoknak. A fogalmak vagy mentális objektumok világán belül a reprodukálható tulajdonságokkal rendelkező fogalmakat matematikai objektumoknak hívjuk, a matematika pedig nem más, mint reprodukálható tulajdonságokkal rendelkező mentális objektumok tanulmányozása. Az intuíció az a képesség, amely lehetővé teszi ezen belső, mentális objektumok vizsgálatát és mérlegelését.
Saját intuícióm és az olvasóé között mindig van némi eltérés. Az egyetértést a kölcsönös alkalmazkodás állandó folyamata hozza létre. Az új kérdések a struktúra új területeire világítanak rá. Előfordul, hogy egy kérdésre nincs válasz. […]
Jól tudjuk, hogy a fizikai világ tárgyaival kapcsolatban vannak nem megválaszolható kérdések, például az, amely egyszerre firtatja az elektron sebességét és helyzetét. De kérdezhetnénk azt is, hány fa nő ma Szabolcs-Szatmárban. A mentális és fizikai objektumokra vonatkozó, megválaszolhatónak tűnő kérdésekről egyaránt kiderülhet – sokszor persze nehézségek árán –, hogy valójában nem megválaszolhatók. Ez azonban még nem kérdőjelezi meg létében az adott mentális vagy fizikai objektumot. Vannak megfelelő kérdések is, amelyekre létezik válasz."
Reuber Hersh: A matematika természete
Typotex Kiadó, 2000
70. oldal
Amiről nem lehet beszélni, arról hallgatni kell, mondja Wittgenstein, a matematikus ezzel szemben bebizonyítja, hogy bizonyos kérdésekre nincs helyes válasz, és ezt is válasznak tekinti.
 Az USA-ban az öt leggyakoribb családnév a Smith, Johnson, Williams, Jones és Brown. Ha megvizsgáljuk az e neveket viselők házassági kapcsolatait, akkor azt a meglepő tényt tapasztalhatjuk, hogy jelentős többségükben olyan párt választanak maguknak, aki ugyan azt a vezetéknevet viselik. (Azaz a házaspárok eredeti neve legtöbbször: Smith-Smith, Johnson-Johnson, Williams-Williams, Jones-Jones és Brown-Brown.) Ez nyilván nem tudatos választás, csupán egy érdekes példa a tudattalan működésére, amely ez esetben a hasonlóhoz vonzódást mutatja. (Az egy tovább vizsgálandó kérdés volna, hogy az azonos nevű emberek -a nevükön túl – másban is hasonlítanak-e egymásra.)
Az USA-ban az öt leggyakoribb családnév a Smith, Johnson, Williams, Jones és Brown. Ha megvizsgáljuk az e neveket viselők házassági kapcsolatait, akkor azt a meglepő tényt tapasztalhatjuk, hogy jelentős többségükben olyan párt választanak maguknak, aki ugyan azt a vezetéknevet viselik. (Azaz a házaspárok eredeti neve legtöbbször: Smith-Smith, Johnson-Johnson, Williams-Williams, Jones-Jones és Brown-Brown.) Ez nyilván nem tudatos választás, csupán egy érdekes példa a tudattalan működésére, amely ez esetben a hasonlóhoz vonzódást mutatja. (Az egy tovább vizsgálandó kérdés volna, hogy az azonos nevű emberek -a nevükön túl – másban is hasonlítanak-e egymásra.) „Az a közeg határozza meg, hogy mit tartasz követendőnek, mit tűrsz el, és hogyan ítélkezel mások felett, amelyben létezel.” – írja Pőcze Flóra (147. o.), és ebben nincs igaza. Ez a rabszolgaerkölcs, amely nem sokkal jobb rabszolgatartó erkölcsénél.*
„Az a közeg határozza meg, hogy mit tartasz követendőnek, mit tűrsz el, és hogyan ítélkezel mások felett, amelyben létezel.” – írja Pőcze Flóra (147. o.), és ebben nincs igaza. Ez a rabszolgaerkölcs, amely nem sokkal jobb rabszolgatartó erkölcsénél.* A könyvben ismertetett pedagógiai program rémesen elavult* (a megjelenés éve 2010): semmi poroszos tekintélyelvűség, semmi rasszizmus. A bűnöző kölköket szeretettel és speciális pszichológiai-pedagógiai szakértelemmel segítendő gyerekeknek tekinti. Jellemző például, hogy a kötet egyik szerzője ilyen kijelentésre ragadtatja magát:
A könyvben ismertetett pedagógiai program rémesen elavult* (a megjelenés éve 2010): semmi poroszos tekintélyelvűség, semmi rasszizmus. A bűnöző kölköket szeretettel és speciális pszichológiai-pedagógiai szakértelemmel segítendő gyerekeknek tekinti. Jellemző például, hogy a kötet egyik szerzője ilyen kijelentésre ragadtatja magát:  James Ellroy
James Ellroy  A posztmodern szerzők kedvenc szokása, hogy összekutyulnak mindent, ami a kezük ügyébe akad, aztán a szegény olvasó tanácstalanul válogathat, mi is az, ami ebből fontos, mi is az, ami csak átverés, mi is az, ami csak szórakoztat?
A posztmodern szerzők kedvenc szokása, hogy összekutyulnak mindent, ami a kezük ügyébe akad, aztán a szegény olvasó tanácstalanul válogathat, mi is az, ami ebből fontos, mi is az, ami csak átverés, mi is az, ami csak szórakoztat? 
 Egy hívő tudós* és irodalmár** okos és szép meditációi, azaz esszéi a világról.
Egy hívő tudós* és irodalmár** okos és szép meditációi, azaz esszéi a világról. Az előbb beszéltem Robert De Niróval (magyar hangja: Reviczky Gábor), aki azt mondta: – Figyelj Mr. vargarockzsolt! Te ezt a szart olvasod? Te egy kibaszott hős vagy! De megdumáltam vele, hogy nem is annyira rossz, és ha 30 évvel fiatalabb és 30 kilóval hájasabb volna, akkor el is játszhatná a főszereplőt.
Az előbb beszéltem Robert De Niróval (magyar hangja: Reviczky Gábor), aki azt mondta: – Figyelj Mr. vargarockzsolt! Te ezt a szart olvasod? Te egy kibaszott hős vagy! De megdumáltam vele, hogy nem is annyira rossz, és ha 30 évvel fiatalabb és 30 kilóval hájasabb volna, akkor el is játszhatná a főszereplőt. Figyelj, haver! Az rendben van, hogy együtt fociztunk a Városligetben, meg a Közgáz Jazz Klubban együtt hallgattuk a legprímább zenéket – például Konrad Bauer, ROVA, meg ilyenek, amik akkor a legmenőbbek voltak, nem csak Európában… (De te már akkor is csak egy kis senki voltál, azóta meg főleg. Ezt nem azért gondolom, mintha lenéznélek, csak éppen más világban mozgunk. Különben szívesen beszélgetek veled, jó csóka vagy, és nem tehetsz róla, hogy ÉN egy állami vállalat VEZÉRIGAZGATÓja lettem, te pedig csak kishivatalnok, aktakukac, bérrabszolga).
Figyelj, haver! Az rendben van, hogy együtt fociztunk a Városligetben, meg a Közgáz Jazz Klubban együtt hallgattuk a legprímább zenéket – például Konrad Bauer, ROVA, meg ilyenek, amik akkor a legmenőbbek voltak, nem csak Európában… (De te már akkor is csak egy kis senki voltál, azóta meg főleg. Ezt nem azért gondolom, mintha lenéznélek, csak éppen más világban mozgunk. Különben szívesen beszélgetek veled, jó csóka vagy, és nem tehetsz róla, hogy ÉN egy állami vállalat VEZÉRIGAZGATÓja lettem, te pedig csak kishivatalnok, aktakukac, bérrabszolga).  MILYENEK AZ ALTERNATÍV ISKOLÁK?
MILYENEK AZ ALTERNATÍV ISKOLÁK?  Ez volt a dolga. Aki ilyet tud, annak meg kell írnia.
Ez volt a dolga. Aki ilyet tud, annak meg kell írnia. 


 Normális országban a költészet súlytalan.* 1971-ben, amikor ez a kötet megjelent, Magyarországon éppen komcsi diktatúra volt. Ez akkoriban normálisnak számított Kelet-Közép-Európában, és akik ezt kritizálták, azok tűntek abnormálisnak. Három éve véget ért a Prágai Tavasz, amely az utolsó kísérlet volt a szocializmus humanizálására. (Fából vaskarika.)
Normális országban a költészet súlytalan.* 1971-ben, amikor ez a kötet megjelent, Magyarországon éppen komcsi diktatúra volt. Ez akkoriban normálisnak számított Kelet-Közép-Európában, és akik ezt kritizálták, azok tűntek abnormálisnak. Három éve véget ért a Prágai Tavasz, amely az utolsó kísérlet volt a szocializmus humanizálására. (Fából vaskarika.)  Önvallomás és beavatás.
Önvallomás és beavatás. 





 Tudod, Picasso az a fazon, akiről a Picasso kalandjai című filmet csinálták, ami marha jó, baromi sokat lehet röhögni rajta. Ezen a könyvön nem nagyon lehet röhögni, pedig elég érdekes nőci írta. Gertude Stein amerikai írónő volt, aki Párizsban élt, és szerintem ezen a könyvén kívül soha nem olvasott tőle senki semmit. De nem ezért volt érdekes – elég sok olyan írónő van, akitől semmit sem olvas az ember, és ezek nem is érdekesek, mint pl. a Vass Virág, Fejős Éva, Szabó Magda vagy Vavyan Fable – hanem mert volt neki egy szalonja, ahová költők, írók, meg festők jártak, pl. Matisse (ő festő), Apollianire (ő költő), meg Hemingway (ő író). Ezek a fazonok a 20. század elején voltak nagymenők, és őrültek is voltak, meg bohémok, ami azt jelenti, hogy kifejezetten normális csókák voltak, és nyugodtan odaülhetnének a Treffortban vagy a Pótkulcsban az asztalodhoz, nem zavarnád el őket, mert még nőket is vonzanának, és ha tudnának magyarul vagy angolul, akkor még normálisan el is lehetne velük beszélgetni. Mondjuk pénzük az nem nagyon volt, pedig most a cuccaik után járó jogdíjakból millió eurókat lehetne kaszálni, de akkor még elég csórók voltak, mert még nem fedezték fel őket.
Tudod, Picasso az a fazon, akiről a Picasso kalandjai című filmet csinálták, ami marha jó, baromi sokat lehet röhögni rajta. Ezen a könyvön nem nagyon lehet röhögni, pedig elég érdekes nőci írta. Gertude Stein amerikai írónő volt, aki Párizsban élt, és szerintem ezen a könyvén kívül soha nem olvasott tőle senki semmit. De nem ezért volt érdekes – elég sok olyan írónő van, akitől semmit sem olvas az ember, és ezek nem is érdekesek, mint pl. a Vass Virág, Fejős Éva, Szabó Magda vagy Vavyan Fable – hanem mert volt neki egy szalonja, ahová költők, írók, meg festők jártak, pl. Matisse (ő festő), Apollianire (ő költő), meg Hemingway (ő író). Ezek a fazonok a 20. század elején voltak nagymenők, és őrültek is voltak, meg bohémok, ami azt jelenti, hogy kifejezetten normális csókák voltak, és nyugodtan odaülhetnének a Treffortban vagy a Pótkulcsban az asztalodhoz, nem zavarnád el őket, mert még nőket is vonzanának, és ha tudnának magyarul vagy angolul, akkor még normálisan el is lehetne velük beszélgetni. Mondjuk pénzük az nem nagyon volt, pedig most a cuccaik után járó jogdíjakból millió eurókat lehetne kaszálni, de akkor még elég csórók voltak, mert még nem fedezték fel őket. 






 Kicsit agresszív az érvelése, és néhol akadnak benne meredek (nem kellően alátámasztott) kijelentések is, de nagyon elgondolkodtató könyv. A két fontos gondolatmenetét idézem:
Kicsit agresszív az érvelése, és néhol akadnak benne meredek (nem kellően alátámasztott) kijelentések is, de nagyon elgondolkodtató könyv. A két fontos gondolatmenetét idézem:
